Labyrinthes
Friday 25 august 2023
Friday 25 august 2023

Nous nous intéressons aux labyrinthes définis au sein d’une grille
30x30. Nous les représenterons en Python par des ensembles de paires
d’entiers compris entre 0 et 29, paires qui désignent les coordonnées
des cellules vides (traversables) du labyrinthe. La paire
(0, 0) correspond au coin en haut à gauche de la
grille.

Examinez les fichiers du dossier 📁 mazes.
Chargez le texte des ces fichiers.
Reconstituez les objets labyrinthes (ensembles de paires)
associés. Nommez random_maze le labyrinthe du fichier
"random-maze.py".
Pour obtenir le labyrinthe du fichier
"random-maze.py":
filename = "mazes/random-maze.py"
file = open(filename, mode="rt", encoding="utf-8")
random_maze_repr = file.read()
file.close()
random_maze = eval(random_maze_repr)Développez avec pygame une fonction display_maze de
visualisation de labyrinthe.
# Pygame
import pygame as pg
# Constants
WIDTH, HEIGHT = 30, 30
CELL_SIZE = 20
FPS = 10
WHITE = (255, 255, 255)
BLACK = (0, 0, 0)
def draw_background(screen):
screen.fill(BLACK)
def draw_walls(screen, maze):
h = CELL_SIZE
for x, y in maze:
pg.draw.rect(screen, WHITE, (x * h, y * h, h, h))
def display_maze(maze):
pg.init()
pg.display.set_caption("Labyrinthes")
width_height = (WIDTH * CELL_SIZE, HEIGHT * CELL_SIZE)
screen = pg.display.set_mode(width_height)
clock = pg.time.Clock()
while True:
events = pg.event.get()
if any(event.type == pg.QUIT for event in events):
break
draw_background(screen)
draw_walls(screen, maze)
pg.display.update()
clock.tick(FPS)
pg.quit()… puis ajoutez-les à la biblothèque existante !
Par exemple pour créer un labyrinthe sans mur :
empty_maze = set()
for y in range(0, HEIGHT):
for x in range(0, WIDTH):
empty_maze.add((x, y))Puis pour le sauvegarder
empty_maze_repr = repr(empty_maze)
file = open("mazes/empty_maze.py", mode="wt", encoding="utf-8")
file.write(empty_maze_repr)
file.close()🏷️ Un graphe (orienté et pondéré) est un triplet composé :
d’un ensemble de sommets ou noeuds (🇺🇸 vertices),
d’un ensemble d’arêtes (orientées) ou arcs (🇺🇸 edges). Une arête orientée est une paire composée d’un sommet source et d’un sommet cible.
d’une collection associant à chaque arête une valeur numérique appelée poids (🇺🇸 weight).
🏷️ Un chemin d’un graphe est une suite de sommets du graphe tels que chaque élément de la suite et son successeur forment une arête du graphe.
On souhaite associer à un labyrinthe un graphe dont
les sommets sont les cellules vides du labyrinthe,
les arêtes représentent les déplacements admissibles d’une cellule à une cellule voisine (les deux cellules sont vides et partagent un coté).
le poids de chaque arête est 1 ; il représente le “coût” du déplacement d’une cellule à une cellule voisine.
Quelle structure de données Python utiliserait-t’on naturellement pour représenter ces graphes ? ⚠️ On ne cherche pas ici la structure la plus compacte ou performante mais à traduire aussi litéralement que possible la description mathématique du graphe.
Implémentez une fonction maze_to_graph qui construit le
graphe associé à un labyrinthe.
Il semble naturel de représenter les sommets comme un ensemble de paires d’entiers, les arêtes comme un ensemble de paires de sommets et les poids comme un dictionnaire ayant comme clés les arêtes et comme valeur unique l’entier 1.
def maze_to_graph(maze):
vertices = set(maze)
edges = set()
weights = {}
for vertex in vertices:
x, y = vertex
for (dx, dy) in [(-1, 0), (0, -1), (1, 0), (0, 1)]:
neighbor = (x + dx, y + dy)
if neighbor in vertices:
edge = (vertex, neighbor)
edges.add(edge)
weights[edge] = 1
return (vertices, edges, weights)Implémentez une fonction reachable_cells qui renvoie
l’ensemble des cellules d’un labyrinthe maze qui sont
atteignables depuis la cellule source.
Etendez la fonction display_maze pour différencier
graphiquement un ensemble de cellules. Puis utilisez-là pour représenter
l’ensemble des cellules atteignables depuis le coin en haut à gauche du
labyrinthe random_maze.

def reachable_cells(maze, source):
vertices, edges, _ = maze_to_graph(maze)
todo = {source}
done = set()
while todo:
current = todo.pop()
neighbors = {
v for v in vertices
if (current, v) in edges
}
for n in neighbors:
if n not in done:
todo.add(n)
done.add(current)
return doneLIGHT_GREEN = (128, 255, 128)
def draw_cells(screen):
h = CELL_SIZE
for x, y in cells:
pg.draw.rect(screen, LIGHT_GREEN, (x * h, y * h, h, h))
def display_maze(maze, cells=None):
pg.init()
pg.display.set_caption("Labyrinthes")
width_height = (WIDTH * CELL_SIZE, HEIGHT * CELL_SIZE)
screen = pg.display.set_mode(width_height)
clock = pg.time.Clock()
while True:
events = pg.event.get()
if any(event.type == pg.QUIT for event in events):
break
draw_background(screen)
draw_walls(screen, maze)
if cells is not None:
draw_cells(screen)
pg.display.update()
clock.tick(FPS)
pg.quit()TOP_LEFT = (0, 0)
cells = reachable_cells(random_maze, source=TOP_LEFT)
display_maze(random_maze, cells=cells)Implémentez une fonction path_from qui prend comme
arguments :
maze : un labyrinthe 30x30,
source : une cellule source ,
et renvoie
path : un dictionnaire ayant pour clés des cellules et
pour valeurs des chemins. Le chemin path[target] doit
joindre source et target si
target est atteignable depuis source ; dans le
cas contraire, target ne doit pas être une clé du
dictionnaire.Utilisez cette fonction pour trouvez un chemin joignant les coins en
haut à gauche et en bas à droite du labyrinthe random_maze
et représenter graphiquement le résulat en mettant à jour votre function
display_maze.

Une solution possible consiste à définir :
def path_from(maze, source):
vertices, edges, _ = maze_to_graph(maze)
todo = set()
done = set()
path = {}
if source in maze:
todo.add(source)
path[source] = [source]
while todo:
current = todo.pop()
neighbors = {
v for v in vertices
if (current, v) in edges
}
for n in neighbors:
if n not in done and n not in todo:
path[n] = path[current] + [n]
todo.add(n)
done.add(current)
return pathpuis à étendre notre fonction display_maze de la façon
suivante :
PINK = (255, 128, 128)
def draw_path(screen, path):
h = CELL_SIZE
for x, y in path:
pg.draw.rect(screen, PINK, (x * h, y * h, h, h))
def display_maze(maze, cells=None, path=None):
pg.init()
pg.display.set_caption("Labyrinthes")
width_height = (WIDTH * CELL_SIZE, HEIGHT * CELL_SIZE)
screen = pg.display.set_mode(width_height)
clock = pg.time.Clock()
while True:
events = pg.event.get()
if any(event.type == pg.QUIT for event in events):
break
draw_background(screen)
draw_walls(screen, maze)
if cells is not None:
draw_cells(screen)
if path is not None:
draw_path(screen, path)
pg.display.update()
clock.tick(FPS)
pg.quit()On exploite ensuite ces fonctions de la façon suivante:
target_to_path = path_from(random_maze, TOP_LEFT)
BOTTOM_RIGHT = (WIDTH - 1, HEIGHT - 1)
path = target_to_path[BOTTOM_RIGHT]
display_maze(random_maze, path=path)Etendre à nouveau la fonction display_maze pour qu’elle
accepte comme argument supplémentaire le dictionnaire produit par
path_from et affiche chaque cellule atteignable dans une
couleur dépendant de la longueur du chemin qui y mène.
Exploiter cette fonctionnalité avec le labyrinthe
random_maze avec comme source le coin en haut à gauche.
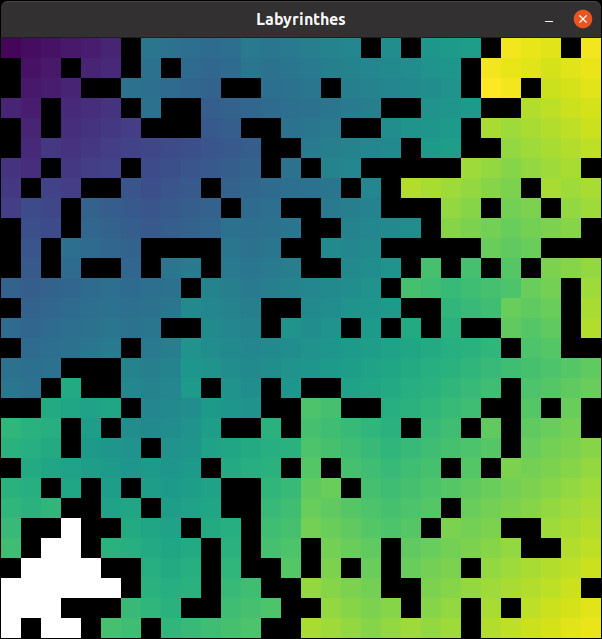
🗝️ On pourra utiliser la fonction colormap suivante qui
associe aux nombres flottants entre 0.0 et 1.0
un triplet RGB d’entiers représentant une couleur exploitable avec
pygame.
import matplotlib.cm # matplotlib colormaps
COLORMAP = matplotlib.cm.viridis
def colormap(x):
x = float(x)
rgba = COLORMAP(x)
rgb = rgba[0:3]
RGB = [min(int(256 * c), 255) for c in rgb]
return RGBassert colormap(0.0) == [68, 1, 84] # purple
assert colormap(0.5) == [32, 145, 140] # turquoise
assert colormap(1.0) == [254, 231, 36] # yellowdef draw_map(screen, map):
h = CELL_SIZE
v_max = max(v for v in map.values())
for (x, y), v in map.items():
pg.draw.rect(
screen,
colormap(float(v / v_max)),
(x * h, y * h, h, h),
)
def display_maze(maze, cells=None, path=None, map=None):
pg.init()
pg.display.set_caption("Labyrinthes")
width_height = (WIDTH * CELL_SIZE, HEIGHT * CELL_SIZE)
screen = pg.display.set_mode(width_height)
clock = pg.time.Clock()
while True:
events = pg.event.get()
if any(event.type == pg.QUIT for event in events):
break
draw_background(screen)
draw_walls(screen, maze)
if cells is not None:
draw_cells(screen, cells)
if map is not None:
draw_map(screen, map)
if path is not None:
draw_path(screen, path)
pg.display.update()
clock.tick(FPS)
pg.quit()map = {
target: len(path) - 1
for target, path in target_to_path.items()
}
display_maze(random_maze, map=map)Pouvez-vous trouvez sur la carte précédente des cibles où le chemin trouvé n’est pas de longueur minimale ?
Implémentez une fonction
shortest_path_from(maze, origin) qui renvoie un
dictionnaire dont les clés sont les cellules atteignables depuis
l’origine et les valeurs un des chemins associés le plus courts
(nécessitant le moins de déplacements) qui joignent la source et la
cible.
Vous pourrez tester votre résultat graphiquement en invoquant
display_maze comme à la question précédente.
Par construction, si à chaque cellule cible le chemin associé est le
plus court possible, les longueurs des chemins entre deux cellules vides
voisines ne peuvent différer que de -1, 0 ou 1. Par conséquent, il
suffit de constater des écarts de couleurs importants entre cellules
voisines de la carte (correspondant à un écart de longueur égal au moins
à deux) pour en conclure qu’on a trouvé un chemin non optimal. Et c’est
bien le cas à quelques endroits sur la carte des longueurs associée à
l’algorithme path_from.
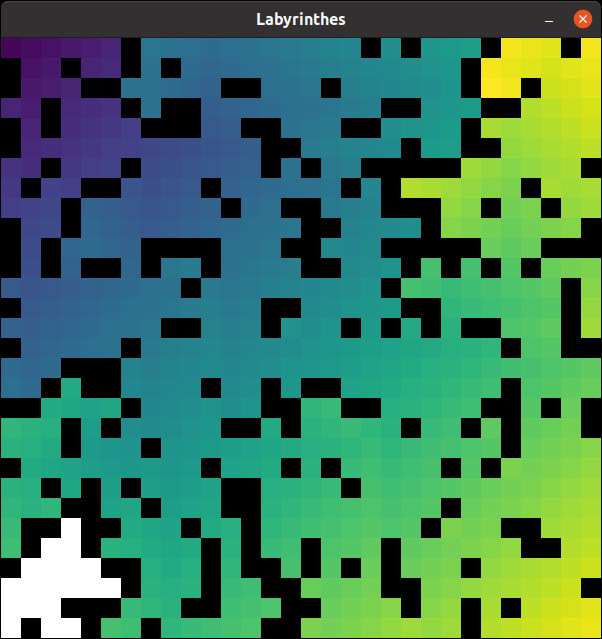
On va donc développer un algorithme nous assurant que la longueur est effectivement minimale.
import math
def shortest_path_from(maze, source):
vertices, edges, weight = maze_to_graph(maze)
distance, path = {}, {}
todo = {source}
distance[source] = 0
path[source] = [source]
while todo:
current = todo.pop()
neighbors = {
v for v in vertices
if (current, v) in edges
}
for n in neighbors:
d = distance[current] + weight[(current, n)]
if d < distance.get(n, math.inf):
distance[n] = d
path[n] = path[current] + [n]
todo.add(n)
return pathOn peut tracer la carte de couleurs correspondantes avec :
target_to_path = shortest_path_from(random_maze, TOP_LEFT)
map = {
target: len(path) - 1
for target, path in target_to_path.items()
}
display_maze(random_maze, map=map)