masques et tableaux booléens¶
ou comment tester en même temps tous les éléments d’un tableau
Nous avons vu les fonctions vectorisées (qui s’appliquent à tout un tableau sans recours à une boucle for-Python). Nous avons aussi vu les fonctions qui aggrègent les valeurs suivant les axes des np.ndarray et permettent par exemple de sommer les lignes ou les colonnes d’une matrice ou encore trouver le plus petit élément ou son index dans la np.ndarray.
Nous allons voir une dernière chose qui consiste à tester tous les éléments d’un np.ndarray (ou bien sûr d’une slice d’un np.ndarray).
Il y a deux manières de tester:
tester tous les éléments et combiner les résultats des tests unitaires en un seul résultat global (le nombre de valeurs paires de votre tableau)
obtenir le
np.ndarrayde booléens résultats des tests individuels (les éléments qui sont pairs)
Nous allons voir rapidement ces deux manières de tester.
import numpy as np
appliquons une condition à un np.ndarray¶
Les conditions s’appliquent à tous les éléments d’un tableau en une seule fois, ce qui signifie que vous ne devez pas écrire de boucle en Python mais laisser les fonctions vectorisées le faire pour vous.
Les opérateurs de comparaison sont des fonctions vectorisées (les fameuses UFuncs). Elles vont retourner un tableau contenant les résultats des comparaisons éléments-par-élément.
Ce tableau est un masque booléen que vous pouvez ensuite utiliser pour filtrer les éléments de votre tableau pour, par exemple, ne garder que ceux pour lesquels la condition est vraie.
On va faire tout de suite un exemple. Construisons une matrice de forme (3 x 4) qui contient des entiers générés aléatoirement entre -10 et 10.
Vous rappelez-vous comment faire une telle matrice ? Essayer avec np.random.randint et reshape:
# votre code ici - la correction ci-dessous
a = np.random.randint(-10, 10, 12).reshape(3, 4)
a
array([[ 2, 8, 9, 4],
[ 9, -4, 9, 0],
[-1, 9, -2, 1]])
Testons la parité des élements (avec le modulo %).
a%2
array([[0, 0, 1, 0],
[1, 0, 1, 0],
[1, 1, 0, 1]])
Comparons les résultats à 0:
a%2 == 0
array([[ True, True, False, True],
[False, True, False, True],
[False, False, True, False]])
Nous obtenons un tableau un masque de booléens.
Les deux manières d’utiliser ce masque sont:
soit de manière globale pour savoir, par exemple, le nombre d’éléments pairs de votre tableau
soit pour filtrer votre matrice initiale, en ne gardant par exemple que les éléments pairs.
prendre le résultat global d’une condition¶
Vous pouvez faire des manipulations, de la matrice des résultats d’une condition, de manière globale avec np.all et np.any - qu’on a déjà rencontrés, rappelez-vous, dans la section sur les agrégations
La permière fonction vous dit si tous les éléments de votre matrice répondent à la condition et la seconde si au moins un élément de votre matrice répond à la condition.
Tous les éléments de la matrice sont-ils pairs ?
np.all(a%2==0)
False
Non (ou alors vous avez une chance incroyable, une chance sur 4096 que ça se produise).
Y-a-t-il au moins un élément pair ?
# sans doute vrai
np.any(a%2==0)
True
Pour information, il existe aussi une fonction qui permet de compter les éléments qui ne sont pas nuls:
np.count_nonzero(a%2==0)
6
filtrer les éléments d’un tableau par une condition¶
Reprenons notre matrice des 12 entiers générés aléatoirement entre -10 et 10. Nous ne voulons garder que les éléments pairs de notre matrice.
Générons le masque booléen des nombres pairs:
pairs = (a%2==0)
pairs
array([[ True, True, False, True],
[False, True, False, True],
[False, False, True, False]])
Ce masque a naturellement la même forme que votre matrice. Pour ne garder que les éléments pairs, (on dit qu’on filtre les éléments de la matrice par ce masque de booléens), nous allons indexer la matrice par ce masque:
# cette construction n'est pas anodine
# l'expression dans les [] est **elle-même un tableau** !
a[a%2==0] # ou faire a[pairs]
array([ 2, 8, 4, -4, 0, -2])
# comme on peut le voir ici
type(pairs)
numpy.ndarray
type(a[pairs])
numpy.ndarray
Vous avez obtenu un nouveau tableau de type np.ndarray qui contient les éléments pairs. Maintenant essayons de composer les conditions sous forme d’une expression logique (e.g. pour faire des et ou des ou et non entre expressions)
composer les conditions¶
Pour composer les conditions
vous devez utiliser les opérateurs logiques bit-à-bit (ou bitwise)
&(pour et),|(pour ou),~(pour non)ou leur contrepartie
numpyqui sont respectivementnp.logical_and,np.logical_or,np.logical_not.
Et vous devez parenthéser les sous-termes de vos expressions.
Si nous voulons les éléments qui ne sont pas pairs et qui sont strictement inférieurs à 6, calculons le masque et indexons notre matrice avec ce masque:
(a < 6) & ~(a%2==0) # le masque
array([[False, False, False, False],
[False, False, False, False],
[ True, False, False, True]])
a[(a < 6) & ~(a%2==0)] # l'indexation du tableau par le masque
array([-1, 1])
Ou en version loooongue
a[np.logical_and(a < 6, np.logical_not(a%2==0))]
array([-1, 1])
mise en garde¶
Cette façon de faire à base d’opérateurs bitwise n’est pas forcément très intuitive…
en Python on aurait eu envie d’utiliser par exemple les opérateurs and et not, au lieu de & et ~
Il ne faut pas le faire, et ça ne fonctionne pas de toutes façons (les opérateurs logiques Python and, or et not ne sont PAS vectorisés)
# au lieu de (a < 6) & ~(a%2==0)
# on pourrait avoir envie d'écrire
(a < 6) and not (a%2==0)
# mais ça ne marche pas...
---------------------------------------------------------------------------
ValueError Traceback (most recent call last)
/tmp/ipykernel_1885/3948634469.py in <module>
1 # au lieu de (a < 6) & ~(a%2==0)
2 # on pourrait avoir envie d'écrire
----> 3 (a < 6) and not (a%2==0)
4
5 # mais ça ne marche pas...
ValueError: The truth value of an array with more than one element is ambiguous. Use a.any() or a.all()
compter les éléments répondant à une condition¶
Nous allons compter les éléments répondant à une condition:
# on pourrait à la rigueur utiliser sum() aussi
np.count_nonzero((a < 6) & ~(a%2==0))
2
Et naturellement vous pouvez compter ces éléments le long des axes de votre np.ndarray. Par exemple pour avoir le nombre d’éléments impairs inférieurs à 6 de chaque colonne, je vais travailler dans l’axe des lignes (axe 0 ici):
np.count_nonzero((a < 6) & ~(a%2==0), axis=0)
array([1, 0, 0, 1])
Si on veut le nombre d’éléments impairs inférieurs à 6 dans les lignes, je vais compter dans l’axe des colonnes:
np.count_nonzero((a < 6) & ~(a%2==0), axis=1)
array([0, 0, 2])
Et maintenant que nous avons extrait les éléments d’un np.ndarray avec une condition, donnons-lui un nom et essayons de modifier un de ses éléments. Faisons simple, prenons le tableau des éléments négatifs et modifions (si il existe) le premier.
nouveau_tableau = a[a<0]
nouveau_tableau
array([-4, -1, -2])
nouveau_tableau[0] = -999
nouveau_tableau
array([-999, -1, -2])
Notre nouveau_tableau est bien modifié. Pensez-vous qu’il en soit de même dans la matrice d’origine ? Non, ce np.ndarray est un tableau complètement différent où les éléments de la matrice d’origine ont été recopiés ! Ce n’est pas une vue sur le tableau d’origine. Pour le voir affichons-le:
a
array([[ 2, 8, 9, 4],
[ 9, -4, 9, 0],
[-1, 9, -2, 1]])
Si nous voulions modifier les éléments de la matrice d’origine vous devez les repérer par leurs indices.
Nous allons prendre les indices de ces éléments dans la matrice d’origine, accéder à ces eléments et les modifier les modifier.
calculer les indices des éléments dans le tableau d’origine¶
Nous venons de voir que quand nous “isolons” les éléments, d’une matrice, qui obéissent à une condition, ils sont recopiés dans un nouvel np.ndarray et nous ne pouvons pas les modifier à partir de ce nouveau tableau.
Si nous voulons accéder aux éléments, qui obéissent à la condition, dans la matrice d’origine: il faut passer par leurs indices.
Ainsi il va nous falloir des fonctions qui nous retournent les indices de ces éléments. Non, il n’est toujours pas question de le faire à-la-main en parcourant le np.ndarray avec des boucles for-Python: ce serait beaucoup trop cher en temps.
Nous allons voir plusieurs manières de faire.
la fonction np.nonzero¶
La fonction np.nonzero renvoie les indices des éléments, qui ne sont pas False ou 0, sous la forme d’un tuple de liste d’indices, le tuple étant de la même dimension que le tableau.
Par exemple si notre tableau num.ndarray est de dimension 2: la fonction renvoie deux listes d’indices, la première liste contient les indices des lignes et la seconde des colonnes.
À vous de jouer. Créez une matrice b de taille (3, 4) qui contient les entiers entre 1 et 12. Créez le masque des éléments qui sont divisibles par 3 et appliquez la fonction np.nonzero à ce masque.
Que devez-vous obtenir ? Les éléments 3, 6, 9, 12 étant respectivement aux indices (0, 2), (1, 1), (2, 0) et (2, 3), si on sépare les indices de lignes et les indices de colonne, on obtient un tuple contenant les deux ndarray (0, 1, 2, 2) et (2, 1, 0, 3).
Essayez de le faire:
# votre code ici (la correction ci-dessous)
# la correction
b = np.arange(1, 13).reshape(3, 4)
b
array([[ 1, 2, 3, 4],
[ 5, 6, 7, 8],
[ 9, 10, 11, 12]])
view_index = np.nonzero(b%3==0)
# comme b est de dimension 2,
# view_index est un tuple de 2 ndarray
view_index
(array([0, 1, 2, 2]), array([2, 1, 0, 3]))
C’est là que ça devient un peu magique
car si je prends la matrice b, je peux l’indicer avec ce tuple et créer ainsi une vue sur la matrice b qui ne contient QUE les éléments qui nous intéressent et les modifier !
b[view_index] # voila les éléments
array([ 3, 6, 9, 12])
Que je peux donc modifier !
b[view_index] = b[view_index] * 10
b
array([[ 1, 2, 30, 4],
[ 5, 60, 7, 8],
[ 90, 10, 11, 120]])
Voila qui est bien utile pour créer une vue sur un ensemble d’arbitraire d’éléments donnés par leurs indices.
la fonction np.argwhere¶
La fonction np.argwhere renvoie les indices des éléments pour lesquels un masque est vrai. Elle renvoie un tableau (np.ndarray), de dimension 2, avec autant de lignes que d’éléments qui matchent et chaque ligne donne les index de l’élément dans chacune des colonnes de la matrice d’origine.
si on cherche les éléments pairs de la matrice $\begin{bmatrix} [1 & 2 & 3] \ [4 & 5 & 6] \end{bmatrix}$ on obtient le np.ndarray suivant $\begin{bmatrix}[ 0&1 ]\ [1&0]\ [1&2]\end{bmatrix}$
aux = np.array([[1, 2, 3], [4, 5, 6]])
aux
array([[1, 2, 3],
[4, 5, 6]])
np.argwhere(aux%2==0)
array([[0, 1],
[1, 0],
[1, 2]])
En fait donc les deux utilitaires np.nonzero et np.argwhere font à peu près le même travail, simplement les coordonnées des points qui matchent sont retournés dans des formats qui sont différents
# si on reprend l'exemple précédent
b = np.arange(1, 13).reshape(3, 4)
b
array([[ 1, 2, 3, 4],
[ 5, 6, 7, 8],
[ 9, 10, 11, 12]])
# le résultat de nonzero
# est un tuple conçu
# pour pouvoir créer une vue
np.nonzero(b%3==0)
(array([0, 1, 2, 2]), array([2, 1, 0, 3]))
# le résultat de argwhere est
# disons plus *human-friendly*
np.argwhere(b%3==0)
array([[0, 2],
[1, 1],
[2, 0],
[2, 3]])
# remarquez que pour reconstruire le résultat de argwhere
# à partir de celui de nonzero
# on pourrait faire par exemple
list(zip(*view_index))
[(0, 2), (1, 1), (2, 0), (2, 3)]
À vous de jouer. Faites un tableau de dimension 3 de taille (2, 3, 4) initialisé avec les entiers de 1 à 25 et demandez les indices des nombres divisibles par 5.
Imprimer le masque et sa forme:
# votre code ici (la correction dessous)
# la correction
a = np.arange(1, 25).reshape(2, 3, 4)
a%5 == 0
array([[[False, False, False, False],
[ True, False, False, False],
[False, True, False, False]],
[[False, False, True, False],
[False, False, False, True],
[False, False, False, False]]])
indices = np.argwhere(a%5==0)
indices
array([[0, 1, 0],
[0, 2, 1],
[1, 0, 2],
[1, 1, 3]])
# il y a 4 points qui matchent
# et pour chacun 3 dimensions, c'est pourquoi
indices.shape
(4, 3)
Il n’y a pas de manière directe d’indices votre tableau a par ces indices, il faudrait reconstruire le tuple des listes d’indices dans toutes les dimensions.
Ici il faudrait reconstruire: ([0, 0, 1, 1], [1, 2, 0, 1], [0, 1, 2, 3]) et faire:
a[([0, 0, 1, 1], [1, 2, 0, 1], [0, 1, 2, 3])] # oui on utilise un tuple de listes et pas de ndarray
array([ 5, 10, 15, 20])
Maintenant que vous avez calculé les indices des éléments divisibles par 5 de votre tableau a, comment atteindre ces éléments dans la matrice a ?
À vous de jouer. Essayez, à partir du tableau indices de modifier les éléments de votre tableau a (par exemple pour les remplacer par 999).
# votre code ici (une correction ci-dessous)
# une correction
a[tuple(indices[:, i] for i in range(indices.shape[1]))]
array([ 5, 10, 15, 20])
# une autre correction qui utilise la transposition de matrice (que nous verrons un peu après)
a[tuple(indices.T)]
array([ 5, 10, 15, 20])
modifier les éléments d’un np.ndarray avec putmask¶
Dans un numpy.ndarray, la fonction np.putmask remplace, les éléments obéissant à un masque, par une valeur donnée en argument. On ne verra que l’exemple avec une valeur unique.
La modification est effectuée dans le tableau (en place).
On va voir l’exemple avec une seule valeur. Construisons un tableau de forme (2, 5) de 10 nombre aléatoires de loi normale $N(0, 1)$ (avec np.random.randn) et remplacons tous les éléments entre -0.5 et 0.5 par 1.
a = np.random.randn(10).reshape(2, 5)
a
array([[-1.5906165 , -1.30331628, 0.41056694, -1.41758467, 1.28576238],
[-0.10729521, -0.54782727, -1.03527082, 0.24554817, -0.10826187]])
np.putmask(a, (-0.5 < a) & (a < 0.5), 0)
a
array([[-1.5906165 , -1.30331628, 0. , -1.41758467, 1.28576238],
[ 0. , -0.54782727, -1.03527082, 0. , 0. ]])
exercices¶
modifier la gaussienne¶
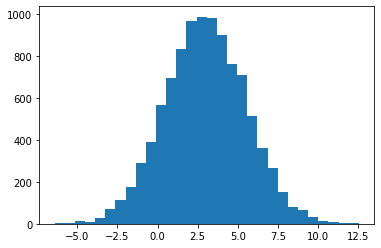
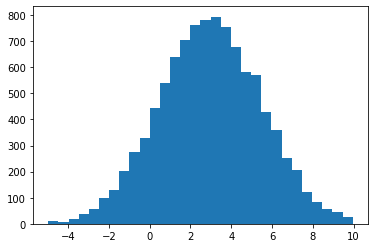
À vous de jouer. Faites un np.ndarray que vous initialisez-le avec des nombres aléatoirement tirés d’une distribution de loi normale de moyenne 3 et de variance 6.25 ($N(3, 6.25)$ avec np.random.randn. Comptez les éléments qui sont inférieurs à -5 ainsi que ceux qui sont supérieurs à 10 et remplacez les tous par la moyenne. Faites le de plusieurs manières différentes.
Avant de commencer, dans la cellule suivante je vous montre comment afficher un histogramme d’un vecteur de points. Afin que nous voyez graphiquement ce qui se passe:
import matplotlib.pyplot as plt
%matplotlib inline
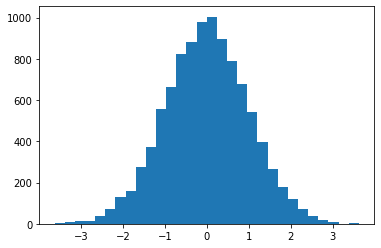
b = np.random.randn(10000)
# vous avez une gaussienne de moyenne 0 et d'écart-type 1
plt.hist(b, bins=30)
(array([4.000e+00, 1.000e+01, 1.300e+01, 1.500e+01, 3.700e+01, 7.200e+01,
1.300e+02, 1.590e+02, 2.740e+02, 3.740e+02, 5.590e+02, 6.630e+02,
8.230e+02, 8.790e+02, 9.770e+02, 1.004e+03, 8.970e+02, 7.880e+02,
6.790e+02, 5.400e+02, 3.970e+02, 2.680e+02, 1.800e+02, 1.210e+02,
7.100e+01, 3.600e+01, 1.900e+01, 7.000e+00, 1.000e+00, 3.000e+00]),
array([-3.63194981, -3.390094 , -3.14823818, -2.90638236, -2.66452654,
-2.42267072, -2.1808149 , -1.93895908, -1.69710326, -1.45524744,
-1.21339162, -0.9715358 , -0.72967998, -0.48782417, -0.24596835,
-0.00411253, 0.23774329, 0.47959911, 0.72145493, 0.96331075,
1.20516657, 1.44702239, 1.68887821, 1.93073403, 2.17258985,
2.41444566, 2.65630148, 2.8981573 , 3.14001312, 3.38186894,
3.62372476]),
<BarContainer object of 30 artists>)